The 4 sum problem is one of the famous problems in Data structures and algorithms that involves finding unique quadruplets that sum up to a given target, which is an extension of the 2 sum and 3 sum problems. In this article, we will understand the problem and explore various approaches to solve the 4 sum problem of leetcode, from the naive brute-force method to more optimized techniques.
What is the 4 sum Problem?
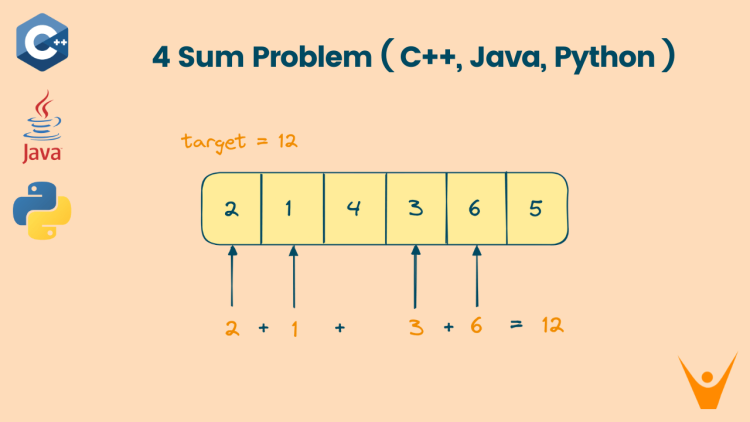
In this problem, we are given an array of numbers and a target value. We have to find quadruplets so that the sum of those 4 numbers is equal to the target value and each quadruplet should consist of distinct elements from the array.
Let us discuss this problem with an example:
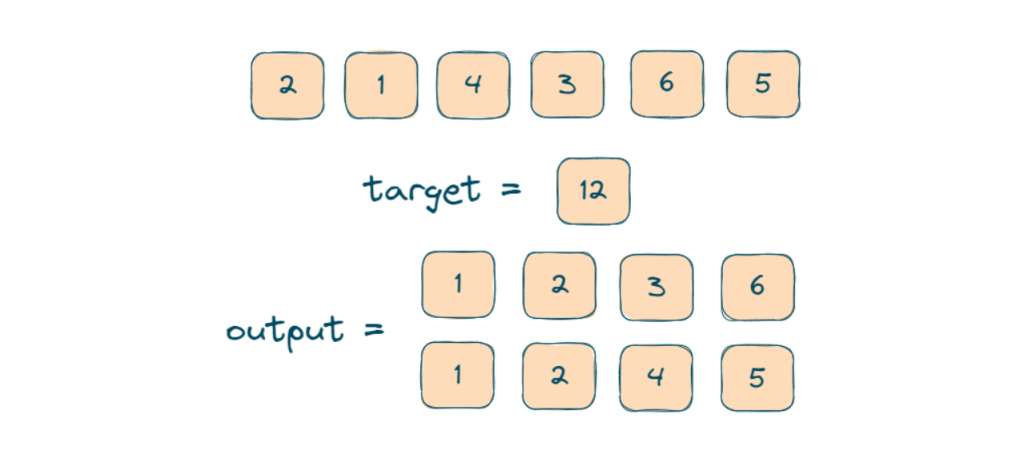
Numbers = [2,1,4,3,6,5]
Target value = 12
We can select the four elements in two ways to get the target = 12. So the unique quadruplets are [1,2,3,6], [1,2,4,5].
Naive Approach: Using four Loops
One of the simple and brute-force approaches to solving the 4 sum problem is using four nested loops. In this approach, we consider all possible combinations of four numbers from the array and check if their sum equals the target value. If, in any iteration, we reach the target, we will add the quadruplet to our result set. We have used a set to obtain unique quadruplets.
Let us understand the naive approach to solve 4 sum problem with the above example:
Numbers = [2,1,4,3,6,5]
Target value = 12
Unique quadruplets are [1,2,3,6], [1,2,4,5]
Steps to be followed for a naive approach:
- We will declare a set data structure first just to return only unique quadruplets
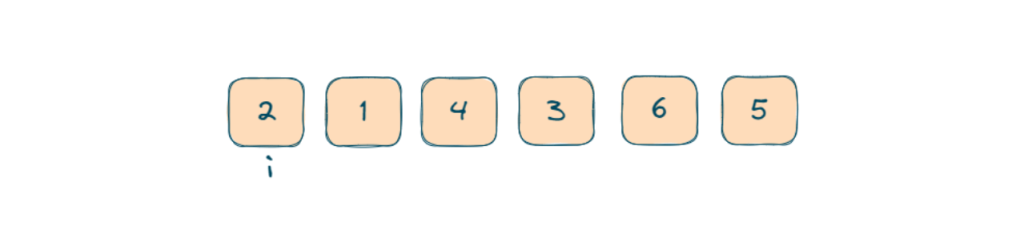
- Now we will start our first loop i from 0 to n-1 (n is the size of the numbers array
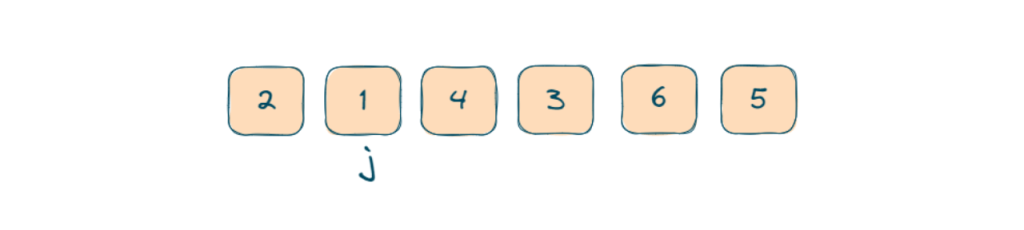
- We will start our second j in the first loop from i+1 to n-1
- Now our third loop k we will start in loop j from j+1 to n-1.
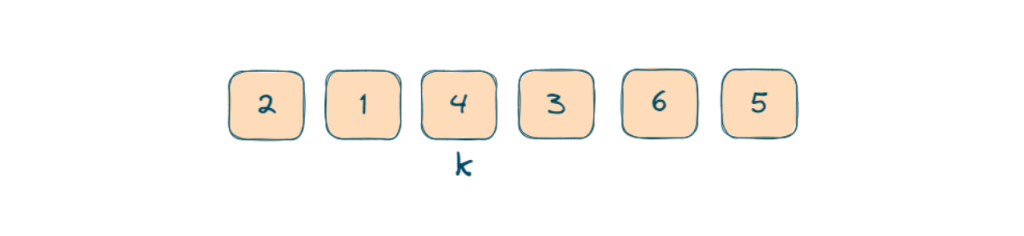
- Now fourth loop l we will start in loop k from k+1 to n-1.
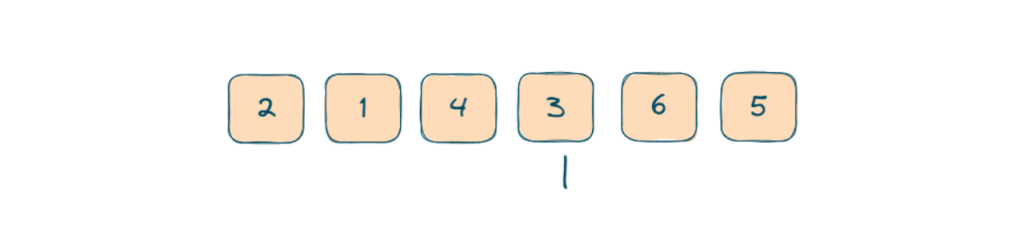
- Now inside fourth loop we will do sum = number[i] + number[j] +number[k] + number[l]
- If the sum is equal to the target then we will sort the quadruplet and insert it in our set
The time complexity for the naive approach is O(n4) because we may need to visit each combination at least once here. The space complexity for this approach is O(n*number of quadruplets) because we are inserting our quadruplets in this set data structure
Better Approach: Using three Loops
This approach is an optimized version of the brute force approach. In this, we will use three loops to find the triplet and obtain the last number of quadruplets by subtracting the sum of the triplet from the target value.
Let us understand this with an example:
Numbers = [2,1,4,3,6,5]
Target value = 12
Unique quadruplets are [1,2,3,6], [1,2,4,5]
For example, if we have 1,2,3 from the first quadruplet and 1,2,4 from the second quadruplet then we are able to find 6 and 5 respectively by subtracting the sum of 1,2,3 and 1,2,4 from target value 12 respectively.
Let us discuss some steps to implement this approach more clearly
- Firstly we will declare a set data structure to store unique quadruplets
- Now we will run our first loop i from 0 to n-1
- Inside our first loop, we will start the second loop from i+1 to n-1.
- Declare a HashSet to store specific array elements for searching the fourth element:
- Now we will use the third loop (k) to iterate from j+1 to n-1.
- Calculate the value of the fourth element (target – (number[i] + number[j] +number[k]))
- If the fourth element is in HashSet then this is the valid fourth element now we will sort our quadruplet and insert it in the set.
- Now we will Insert the nums[k] in the HashSet and repeat the process for all iterations of the third loop.
The time complexity for the naive approach is O(n3*log(M)) because here we are mainly using 3 nested loops where M is the number of elements in the set and some operations are done on the set that takes log(M) time complexity
The space complexity is O(n * no. of the quadruplets)+O(N) for storing unique quadruplets and O(n) by a set data structure that we are using to store array elements
Optimized Approach: 4 Pointer
In the 4 pointer approach to solve the 4 sum problem, we will also use three nested loops but here we will get rid of the time complexity that we are getting from operations on HashSet that we were getting in a better approach.
For this optimized approach we first need to sort our number array.
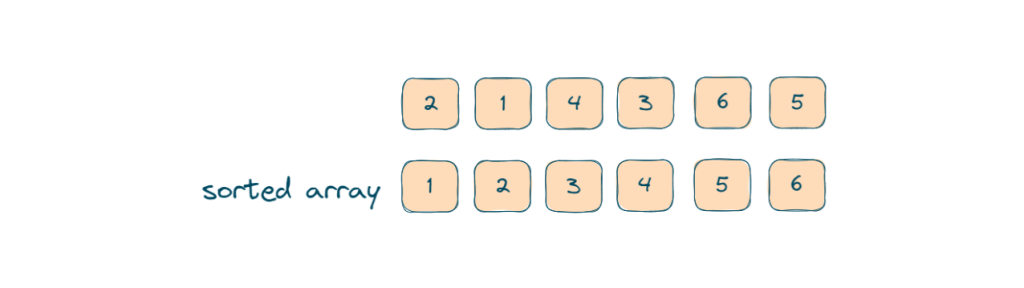
Steps to solve this problem using 4 pointer approach:
- We will use two outer loops for the first two elements and use two pointers in a nested loop fashion to iterate through all possible pairs of the first two elements. These pointers (i and j) will ensure unique combinations.
- Now we will use two inner pointers for the remaining two elements:
- Introduce two more pointers (l and r) inside the nested loops to point to the remaining two elements. These pointers will move toward each other as we adjust the quadruplet sum.
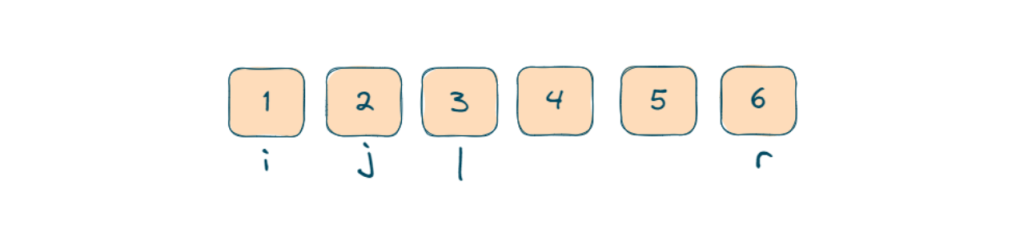
- Here l = j+1 and r = n-1 (n is the size of the number array).
- Now we will check the sum of number[i] + number[j] +number[l] + number[r] 1+2+3+6 = 12 sum is equal to our target then this is our desired quadruplet
- If the sum is greater than the target then we reduce r by 1
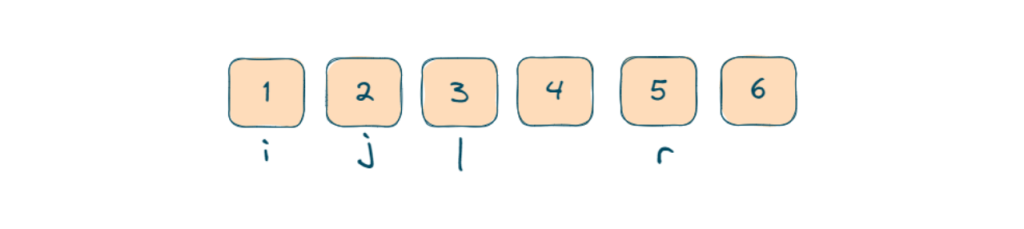
- If the sum is lesser than the target then we will increase l by 1.
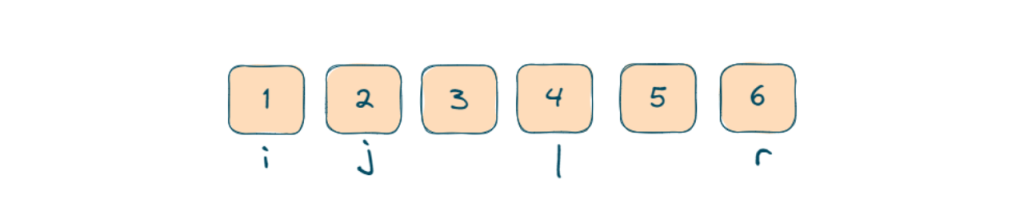
- We will do this while(l<r) after this we will continue the iterations of the outer loops to explore all possible combinations. And again j = i+1 , l = j+1 and r = n-1.
- Duplicate elements are checked within the loop by checking with the previous element and continuing if it is the same so that we can obtain a unique quadruplet.
C++ Code
Below is the C++ program to solve the 4 sum problem:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> result;
int n = nums.size();
if (n < 4) {
return result;
}
sort(nums.begin(), nums.end());
for (int i = 0; i < n - 3; ++i) {
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
for (int j = i + 1; j < n - 2; ++j) {
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
int left = j + 1;
int right = n - 1;
while (left < right) {
long long sum = nums[i];
sum+= nums[j];
sum+= nums[left];
sum+= nums[right];
if (sum == target) {
result.push_back({nums[i], nums[j], nums[left], nums[right]});
while (left < right && nums[left] == nums[left + 1]) {
++left;
}
while (left < right && nums[right] == nums[right - 1]) {
--right;
}
++left;
--right;
}
else if (sum < target) {
++left;
}
else {
--right;
}
}
}
}
return result;
}
int main() {
vector<int> nums = {2, 1, 4, 3, 6, 5};
int target = 12;
vector<vector<int>> result = fourSum(nums, target);
cout << "Quadruplets that sum up to " << target << ":" << endl;
for (const auto& quad : result) {
for (int num : quad) {
cout << num << " ";
}
cout << endl;
}
return 0;
}Python Code
Below is the Python program to solve this DSA problem:
def four_sum(nums, target):
result = []
nums.sort()
for i in range(len(nums) - 3):
if i > 0 and nums[i] == nums[i - 1]:
continue
for j in range(i + 1, len(nums) - 2):
if j > i + 1 and nums[j] == nums[j - 1]:
continue
left = j + 1
right = len(nums) - 1
while left < right:
curr_sum = nums[i] + nums[j] + nums[left] + nums[right]
if curr_sum == target:
result.append([nums[i], nums[j], nums[left], nums[right]])
while left < right and nums[left] == nums[left + 1]:
left += 1
while left < right and nums[right] == nums[right - 1]:
right -= 1
left += 1
right -= 1
elif curr_sum < target:
left += 1
else:
right -= 1
return result
nums = [2, 1, 4, 3, 6, 5]
target = 12
result = four_sum(nums, target)
print("Quadruplets that sum up to", target, ":")
for quad in result:
print(quad)Java Code
Check the Java code to implement the 4 pointers approach:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class FourSum {
public static List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> result = new ArrayList<>();
int n = nums.length;
if (n < 4) {
return result;
}
Arrays.sort(nums);
for (int i = 0; i < n - 3; ++i) {
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
for (int j = i + 1; j < n - 2; ++j) {
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
int left = j + 1;
int right = n - 1;
while (left < right) {
long sum = nums[i];
sum+= nums[j];
sum+= nums[left];
sum+= nums[right];
if (sum == target) {
result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
while (left < right && nums[left] == nums[left + 1]) {
++left;
}
while (left < right && nums[right] == nums[right - 1]) {
--right;
}
++left;
--right;
}
else if (sum < target) {
++left;
}
else {
--right;
}
}
}
}
return result;
}
public static void main(String[] args) {
int[] nums = {2, 1, 4, 3, 6, 5};
int target = 12;
List<List<Integer>> result = fourSum(nums, target);
System.out.println("Quadruplets that sum up to " + target + ":");
for (List<Integer> quad : result) {
System.out.println(quad);
}
}
}Output:
Quadruplets that sum up to 12:
1 2 3 6
1 2 4 5The time complexity of this optimized approach is O(n3), i and j pointers running n times, and combined l and r pointers are also running n time. The space complexity of this optimized approach is O(1).
Here is the comparison analysis of the 3 approaches to solve the 4 sum problem:
| Approaches | Time complexity | Space complexity | Details |
| Naive approach: Using 4 loops | O(n4) | O(n*number of quadruplets) | We consider all possible combinations of four numbers from the array and check if their sum equals the target value. |
| Better approach: Using 3 loops | O(n3*log(M)) | O(n * no.of quadruplets)+O(N) | We use three loops to find the triplet and obtain the last number of quadruplets by subtracting the sum of the triplet from the target value. |
| Optimized approach: Using a Sorted array, 4 pointers | O(n3) | O(1) | We first sort the array and use 4 pointers to find the combinations. |
Conclusion
In conclusion, the optimized 4-pointer approach stands out as the most efficient solution for the 4 sum problem, providing a balance between simplicity and performance. The use of sorting and carefully managed pointers minimizes time complexity to O(n3) while maintaining constant space complexity. This approach is recommended for larger datasets where performance is crucial.