In this article, we will try to solve the 2 keys keyboard problem. It is an interesting leetcode problem because the most efficient way to solve it often requires dynamic programming or mathematical insight to minimize the number of operations. The main idea is to notice the best way to do things in order to get n number of ‘A’. We will figure out how to use the copy and paste operations strategically to reach the desired number of ‘A’s with the minimum steps.
What is the 2 Keys Keyboard Problem?
The problem typically involves a notepad with only one character, ‘A’, initially present, the allowed operations are:
- Copy all the characters on the screen.
- Paste the characters that were copied last time.
The main goal of the 2 keys problem is to find the minimum number of operations needed to obtain exactly ‘n’ ‘A’s on the screen using the copy-and-paste operation
Dynamic Programming Approach
We have a notepad and we can perform two operations copying all the characters and pasting them. We will try to solve it using the dynamic programming.
Let us understand it with an example,
Input: n = 3
Output: 3
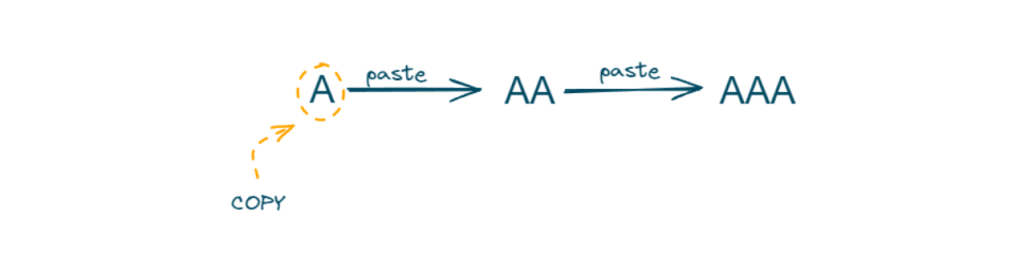
In step 1, we use the Copy All operation.
In step 2, we use the Paste operation to get ‘AA’.
In step 3, we use the Paste operation to get ‘AAA’.
Steps to solve 2 keys keyboard problem:
- Let’s start with the base case, where ‘n’ is 1. In this case, we already have one ‘A’ on the notepad, so no operations are needed. So the answer is 0.
- Now, let’s consider the case where ‘n’ is 2. We will start with one ‘A’. To get two ‘A’s, you can perform a copy and then a paste. So the answer is 2.
- As we go on, we will observe a pattern. For example, to get three ‘A’s, you can copy the one ‘A’ you have and then paste it. To get four ‘A’s, you can copy the two ‘A’s you have and then paste. It’s like doubling the number of ‘A’s each time.
- We will initialize a dp array of size n+1 to follow 1-based indexes to store minimum operations

- Now we will initialize base case dp[1] = 0
![initialize base case dp[1] = 0](https://favtutor.com/articles/wp-content/uploads/2023/11/3-5-1024x222.png)
- We will run two loops to fill the dp array with the minimum value till n
- The outer loop runs from 2 to n, considering each possible count of ‘A’s on the notepad.
- outer loop runs from 2 to n, considering each possible count of ‘A’s on the notepad.
- If i is divisible by j, it means we can copy ‘j’ ‘A’s and paste it i/j times to get ‘i’ ‘A’s.
- The dp[i] is updated with the minimum of its current value and the calculated value using dp[j] + i / j.
- Now dp[n] is our ans as we were storing minimum values always
![answer is dp[n]](https://favtutor.com/articles/wp-content/uploads/2023/11/2-5-1024x270.png)
C++ Code
Below is the complete C++ program to solve the 2 keys keyboard problem:
#include<bits/stdc++.h>
using namespace std;
int minOperations(int n) {
if (n == 1) {
return 0; // Base case: already have one 'A'
}
vector<int> dp(n+1, INT_MAX); // Dynamic programming array to store minimum operations
dp[1] = 0; // Base case
for (int i = 2; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (i % j == 0) {
// If 'i' is divisible by 'j', it means we can copy 'j' 'A's and paste it i/j times to get 'i' 'A's
dp[i] = min(dp[i], dp[j] + i / j);
}
}
}
return dp[n];
}
int main() {
int n = 3;
int result = minOperations(n);
cout << "Minimum number of operations to get " << n << " 'A's: " << result << endl;
return 0;
}Java Code
Check the Java program to solve the problem:
import java.util.Arrays;
public class MinOperations {
public static int minOperations(int n) {
if (n == 1) {
return 0; // Base case: already have one 'A'
}
int[] dp = new int[n + 1];
Arrays.fill(dp, Integer.MAX_VALUE); // Dynamic programming array to store minimum operations
dp[1] = 0; // Base case
for (int i = 2; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (i % j == 0) {
// If 'i' is divisible by 'j', it means we can copy 'j' 'A's and paste it i/j times to get 'i' 'A's
dp[i] = Math.min(dp[i], dp[j] + i / j);
}
}
}
return dp[n];
}
public static void main(String[] args) {
int n = 3;
int result = minOperations(n);
System.out.println("Minimum number of operations to get " + n + " 'A's: " + result);
}
}Python Code
Check the Python program to solve the problem:
def min_operations(n):
if n == 1:
return 0 # Base case: already have one 'A'
dp = [float('inf')] * (n + 1) # Dynamic programming array to store minimum operations
dp[1] = 0 # Base case
for i in range(2, n + 1):
for j in range(1, i):
if i % j == 0:
# If 'i' is divisible by 'j', it means we can copy 'j' 'A's and paste it i/j times to get 'i' 'A's
dp[i] = min(dp[i], dp[j] + i // j)
return dp[n]
if __name__ == "__main__":
n = 3
result = min_operations(n)
print(f"Minimum number of operations to get {n} 'A's: {result}")Output:
Minimum number of operations to get 3 'A's: 3Complexity Analysis
The time complexity for the above code to solve the 2 keys keyboard problem is O(n2) as the outer loop runs ‘n-1’ and the inner loop runs ‘i-1’ times for each iteration of the outer loop and operations inside the loops are taking constant times
The space complexity for the above code is O(n) as we have declared a dp array of size (n+1), the space used scales linearly with the input size n.
Conclusion
The aim of the leetcode problem 2 keys keyboard is to find the minimum number of operations needed to obtain exactly ‘n’ ‘A’s on the screen using the copy-and-paste operation. In this article, we discussed how the dynamic programming approach efficiently solves the problem and we have discussed C++, Java, and Python code to solve this problem.








