In the world of algorithms and problem-solving, the Two Sum problem stands as a classic and fundamental challenge. In this article, we will understand the problem and explore various approaches to solve this problem, from the naive brute-force method to more optimized techniques using sorting and two-pointers.
What is the Two Sum Problem?
Before diving into the solution strategies, it’s essential to grasp the problem’s requirements and constraints. The 2 Sum problem assumes that there exists exactly one solution, and we cannot use the same element twice. The Two Sum problem requires us to find a unique pair of numbers whose sum matches the target value.

Let us consider an array {9, 1, 5, 4, 7}, and the desired sum is 10. As we can see from the illustration above, the element at index 0 is 9, and index 1 is 1, which gives a sum equal to 10. Hence, we can conclude that our answer indices are 0 and 1.
Naive Approach
The naive approach to solving this problem involves iterating through the array and checking every possible pair of numbers. We start with the first number and calculate the sum with each subsequent number. If we find a pair whose sum matches the target, we return their indices. Otherwise, we continue the process until we exhaust all the numbers in the array.
Let’s visualize it with a simple example. Consider an array [1, 2, 2, 7] and a target value of 9. Our goal is to find two numbers within the array that add up to 9.
Let’s apply the naive approach to our example. We begin with the number 1 and compute the sums with the remaining numbers of the array:
1 + 2 = 3
1 + 2 = 3
1 + 7 = 8
None of these sums equal our target value of 9. Moving on, we consider the next number, 2, and repeat the process:
2 + 2 = 4
2 + 7 = 9
Finally, we find a pair that adds up to 9 at indices [1, 3]. It’s important to note that we only compute sums using numbers that come after the current index. This avoids redundant calculations and ensures that we find a unique solution.
The naive approach to solving the Two Sum problem has a time complexity of O(n^2), where n is the size of the input array. This is because we iterate through the array twice, resulting in nested loops. As the array size grows, the execution time increases exponentially. The space complexity is O(1) as we are not using any extra space.
Optimized Approach: Two Pointers
The naive approach is simple but inefficient for larger arrays. We can optimize the Two Sum problem by utilizing sorting and the two-pointer technique. The idea is to sort the array in non-decreasing order, allowing us to apply a more efficient algorithm.
With the sorted array, we can now use the two-pointer technique to find the pair that adds up to the target. The two pointers, one at the beginning and another at the end of the array move towards each other based on the comparison of their sum with the target.
To ensure that we do not lose the index after sorting the array, we will make a vector pair and store the integer values and indexes together.
Let us try to get a good grasp of the technique by dry running using an example.
Let us take the array shown in the illustration above, and try to find two numbers that can be summed up to 11.
- Let’s sort the array in descending order.
- Now let’s place two pointers, one at the beginning of the array and one at the end.
- Now we will make the comparison and move the pointers accordingly.
- If the sum of the integers is less than the target, we will move the j pointer to the left.
- If the sum of the integers is more than the target, we will move the i pointer to the right.
- If the sum of the integers is equal to the target, we have found the right indices.
- The sum of the integers is 10, which is less than the target, hence, we will move the j pointer to the left.
- Now the sum of the integers is 13, which is greater than the target value. Hence, we will move the i pointer to the right.
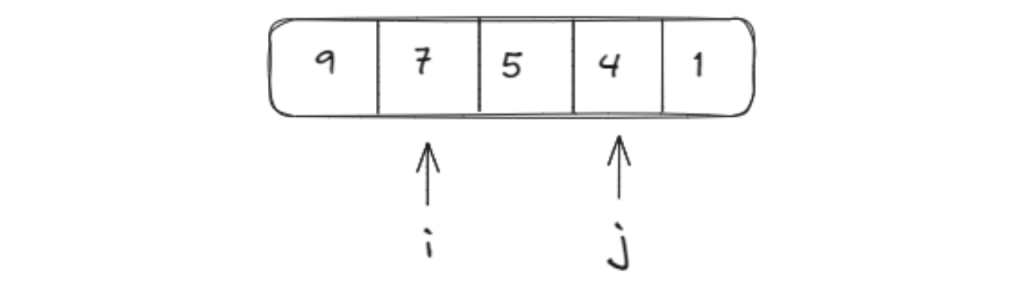
- Now the sum of the integers is 11, which is equal to the target value. Hence, we have found our answer indices.
- Therefore, the indices of the two integers whose sum is equal to 11 are 1 and 3.
C++ Program
Here is the C++ code to solve the two sum problem:
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
/**
* Function to find indices of two numbers that
* add up to the target using two-pointer technique
*/
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> result;
vector<pair<int, int>> numsWithIndex;
// Create a vector of pairs (element, index)
for (int i = 0; i < nums.size(); i++) {
numsWithIndex.push_back({nums[i], i});
}
// Sort the vector based on the element value
sort(numsWithIndex.begin(), numsWithIndex.end());
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int currentSum = numsWithIndex[left].first + numsWithIndex[right].first;
if (currentSum == target) {
// Found the indices, store them in the result vector
result = {numsWithIndex[left].second, numsWithIndex[right].second};
break;
} else if (currentSum < target) {
// Increment the left pointer to increase the sum
left++;
} else {
// Decrement the right pointer to decrease the sum
right--;
}
}
return result;
}
int main() {
vector<int> nums = {9, 1, 5, 4, 7};
int target = 11;
vector<int> result = twoSum(nums, target);
if (!result.empty()) {
cout << "Indices of the two numbers that add up to the target: " << result[0] << ", " << result[1] << endl;
} else {
cout << "No solution found!" << endl;
}
return 0;
}Java Program
Below we provided the Java Code to solve the two sum problem:
import java.util.Arrays;
public class TwoSum {
/**
*Function to find indices of two numbers that
*add up to the target using two-pointer technique
*/
public static int[] twoSum(int[] nums, int target) {
int[] result = new int[2];
int[] sortedNums = Arrays.copyOf(nums, nums.length);
Arrays.sort(sortedNums);
int left = 0;
int right = nums.length - 1;
while (left < right) {
int currentSum = sortedNums[left] + sortedNums[right];
if (currentSum == target) {
// Found the indices, find the original indices and store in the result array
int leftIndex = -1;
int rightIndex = -1;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == sortedNums[left] && leftIndex == -1) {
leftIndex = i;
} else if (nums[i] == sortedNums[right]) {
rightIndex = i;
}
}
result[0] = leftIndex;
result[1] = rightIndex;
break;
} else if (currentSum < target) {
// Increment the left pointer to increase the sum
left++;
} else {
// Decrement the right pointer to decrease the sum
right--;
}
}
return result;
}
public static void main(String[] args) {
int[] nums = {9, 1, 5, 4, 7};
int target = 11;
int[] result = twoSum(nums, target);
if (result[0] != -1 && result[1] != -1) {
System.out.println("Indices of the two numbers that add up to the target: " + result[0] + ", " + result[1]);
} else {
System.out.println("No solution found!");
}
}
}Python Program
Finally, you can also find the Python code to implement the optimized approach:
# Function to find indices of two numbers that
# add up to the target using two-pointer technique
def two_sum(nums, target):
result = []
nums_with_index = [(num, index) for index, num in enumerate(nums)]
# Sort the list of tuples based on the element value
nums_with_index.sort(key=lambda x: x[0])
left, right = 0, len(nums) - 1
while left < right:
current_sum = nums_with_index[left][0] + nums_with_index[right][0]
if current_sum == target:
# Found the indices, store them in the result list
result = [nums_with_index[left][1], nums_with_index[right][1]]
break
elif current_sum < target:
# Increment the left pointer to increase the sum
left += 1
else:
# Decrement the right pointer to decrease the sum
right -= 1
return result
if __name__ == "__main__":
nums = [9, 1, 5, 4, 7]
target = 11
result = two_sum(nums, target)
if result:
print("Indices of the two numbers that add up to the target:", result[0], result[1])
else:
print("No solution found!")Output:
Indices of the two numbers that add up to the target: 3, 4The optimized approach using sorting and the two-pointer technique significantly improves the time complexity of the 2 Sum problem. Sorting the array takes O(n log n) time, and the two-pointers technique requires a single pass through the array, which takes O(n) time. Therefore, the overall time complexity is O(n log n). The space complexity is O(1) as we are not using any extra space.
Analysis of Both Approaches
Let’s see a quick review of both the approaches.
| Approach | Time Complexity | Space Complexity | Details |
| Naive Approach | O(n^2) | O(1) | The naive approach involves iterating through the array and checking all possible pairs of numbers to find the target sum. |
| Two pointer Approach | O(n log n) | O(1) | This approach involves sorting the array in non-decreasing order and using a two-pointer technique to find the pair that adds up to the target. |
Conclusion
In this article, we have discussed the Two Sum problem, which involves finding two indices in an array of integers that add up to a given target value. The code examples in C++, Python, and Java demonstrate how to implement this optimized approach to find the indices of the two numbers that add up to the target.








