Finding a number in a sorted array is the standard question that can be solved through binary search easily. However, the difficulty arises when the question is based on rotated arrays. In this article, we will see various approaches to searching for an element in a Rotated Sorted Array, with solutions implemented in C++, Java, and Python.
Search in a Rotated Sorted Array Problem
In the leetcode problem to Search in a Rotated Sorted array, you are given a rotated sorted array (a sorted array that is rotated at some index). You are also given an integer target which you have to find whether it contains in that array or not. If it is contained in the array, return the index of that position; otherwise, return -1.
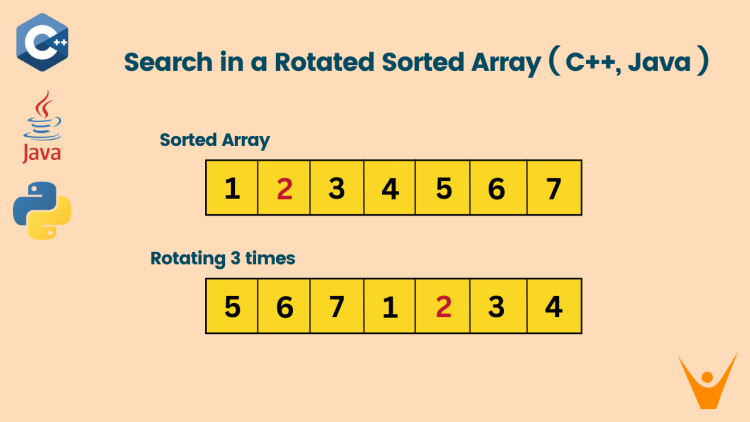
Here is an example of the rotated array, which has been rotated 2 times:
Note that all the values contained in the array are distinct.
Input: array = [2, 3, 4, 0, 1], target = 0
Output: 3 (As 0 lies in the array which is rotated two times.)
Input: array = [2, 3, 4, 1], target = 0
Output: -1 (0 does not lie in the array)
The simplest way to approach this problem is to check each element present in the array with the target. If the target element is present in the array return true, otherwise return false. Here is how to do it:
- First, iterate over each element of the array.
- Check if that element is the same as the target element.
- If they are the same return the index. Otherwise, return -1.
The time complexity here will be O(n) where n is the size of the array. As we are iterating over each element of the array. The space complexity is only O(1) as we are not using any extra space.
Optimized Binary Search Approach
In the above approach, we are iterating over each element present in the array. Instead of iterating over each element, we can take benefit of the sorted array. As the array is sorted but rotated so all the elements present left to the pivot are greater than the elements present on the right side of the pivot.
Now we will first find the pivot element and check if our target element is less than or greater than the last element of the array. If the target element is greater than the last element look at the left side of the pivot. If it is smaller, then look at the right side of the pivot element.
To find the pivot element, you can refer to our solution for finding the minimum in the sorted array.
Let’s examine the approach after finding the pivot element.
- First, check if the target element is smaller than the last element of the array or not.
- If it is smaller than the last element call the binary search function from the pivot to the last index.
- Otherwise, call the binary search function from the starting till index = (pivot-1).
- In the binary search function simply check for the middle index. If the target element is smaller than the current element update end = mid – 1.
- Otherwise, update the starting index to start = mid +1. Keep on iterating till start <= end.
Now you know the process, we just need to code it.
C++ Code
Here is the C++ program to search for an element in a rotated sorted array:
#include<bits/stdc++.h>
using namespace std;
int find_pivot(vector<int>& v){
int start = 0, end = v.size()-1;
int n = v.size()-1;
int pivot = 0;
while(start <= end ){
int mid = (start + end)/2;
if(v[mid] < v[mid-1]) {
pivot = mid;
break;
}
if(v[mid] > v[n-1]) start = mid+1;
else {
end = mid-1;
}
}
return pivot;
}
int binary_search(int start, int end, int target, vector<int>& v){
while(start <= end){
int mid = (start + end)/2;
if(v[mid] == target) return mid;
if(v[mid] < target) start = mid + 1;
else end = mid - 1;
}
return -1;
}
int main(){
vector<int>v = {2, 3, 4, 0, 1};
int target = 4;
int n = v.size();
int pivot_index = find_pivot(v);
cout<<"The pivot index is: "<<pivot_index<<endl;
if(v[n-1]>= target) cout<<binary_search(pivot_index, n-1, target, v);
else cout<<binary_search(0, pivot_index, target, v);
return 0;
}
Java Code
import java.util.*;
public class Main {
public static int findPivot(List<Integer> v) {
int start = 0, end = v.size() - 1;
int n = v.size() - 1;
int pivot = 0;
while (start <= end) {
int mid = (start + end) / 2;
if (v.get(mid) < v.get(mid - 1)) {
pivot = mid;
break;
}
if (v.get(mid) > v.get(n - 1)) start = mid + 1;
else {
end = mid - 1;
}
}
return pivot;
}
public static int binarySearch(int start, int end, int target, List<Integer> v) {
while (start <= end) {
int mid = (start + end) / 2;
if (v.get(mid) == target) return mid;
if (v.get(mid) < target) start = mid + 1;
else end = mid - 1;
}
return -1;
}
public static void main(String[] args) {
List<Integer> v = new ArrayList<>(Arrays.asList(2, 3, 4, 0, 1));
int target = 4;
int n = v.size();
int pivotIndex = findPivot(v);
System.out.println("The pivot index is: " + pivotIndex);
if (v.get(n - 1) >= target) System.out.println(binarySearch(pivotIndex, n - 1, target, v));
else System.out.println(binarySearch(0, pivotIndex, target, v));
}
}Java Code
We can implement the binary search approach in Java also:
import java.util.*;
public class Main {
public static int findPivot(List<Integer> v) {
int start = 0, end = v.size() - 1;
int n = v.size() - 1;
int pivot = 0;
while (start <= end) {
int mid = (start + end) / 2;
if (v.get(mid) < v.get(mid - 1)) {
pivot = mid;
break;
}
if (v.get(mid) > v.get(n - 1)) start = mid + 1;
else {
end = mid - 1;
}
}
return pivot;
}
public static int binarySearch(int start, int end, int target, List<Integer> v) {
while (start <= end) {
int mid = (start + end) / 2;
if (v.get(mid) == target) return mid;
if (v.get(mid) < target) start = mid + 1;
else end = mid - 1;
}
return -1;
}
public static void main(String[] args) {
List<Integer> v = new ArrayList<>(Arrays.asList(2, 3, 4, 0, 1));
int target = 4;
int n = v.size();
int pivotIndex = findPivot(v);
System.out.println("The pivot index is: " + pivotIndex);
if (v.get(n - 1) >= target) System.out.println(binarySearch(pivotIndex, n - 1, target, v));
else System.out.println(binarySearch(0, pivotIndex, target, v));
}
}Python Code
Finally, here is the Python program:
def find_pivot(v):
start, end = 0, len(v) - 1
pivot = 0
while start <= end:
mid = (start + end) // 2
if v[mid] < v[mid - 1]:
pivot = mid
break
if v[mid] > v[-1]:
start = mid + 1
else:
end = mid - 1
return pivot
def binary_search(start, end, target, v):
while start <= end:
mid = (start + end) // 2
if v[mid] == target:
return mid
if v[mid] < target:
start = mid + 1
else:
end = mid - 1
return -1
if __name__ == "__main__":
v = [2, 3, 4, 0, 1]
target = 4
n = len(v)
pivot_index = find_pivot(v)
print("The pivot index is:", pivot_index)
if v[-1] >= target:
print(binary_search(pivot_index, n - 1, target, v))
else:
print(binary_search(0, pivot_index, target, v))
Output:
The pivot index is: 3
2The time complexity is reduced to search in a rotated sorted array by using binary search is O( log(n) ), where n is the size of the array. By always finding the middle element and based on that, we reject either the left or right side, which has reduced our time complexity to O(log(n)). The space complexity is O(1) as we are not using any extra space.
Here is how both the approaches compares:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O(n) | O(1) | We are iterating over each element present in the array. |
| Optimized Approach | O( log(n) ) | O(1) | We are using binary search which reduced our time complexity to O( log n). |
Conclusion
We saw how to Search in a Rotated Sorted Array, a very interesting leetcode problem. We also compare the time and space complexity of various approaches and find out that binary search is the best way to solve these types of questions.