Arrays are always the main data structures you need to master before coding interviews because there can be many interesting leetcode problems that you can have with it. In this article, we will explore one such problem to find the product of array except itself, find an optimal solution, and understand its time and space complexities.
What is the Product of Array Except Self?
Finding the Product of Array Except Itself which requires finding the product of all elements in an array, except for the element at a given index. Without the division operator, this problem can be solved efficiently in O(n) time.
Here is the problem statement: “We are given an array of numbers, and for each element in the array, we need to find the product of all the other elements except itself.“
Let us understand it better with an example:
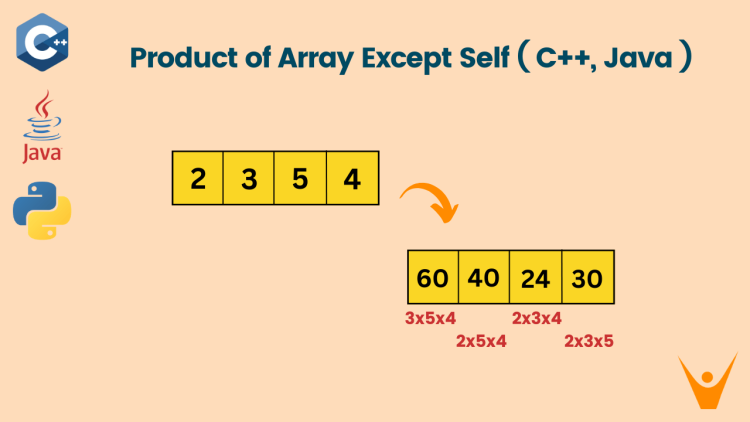
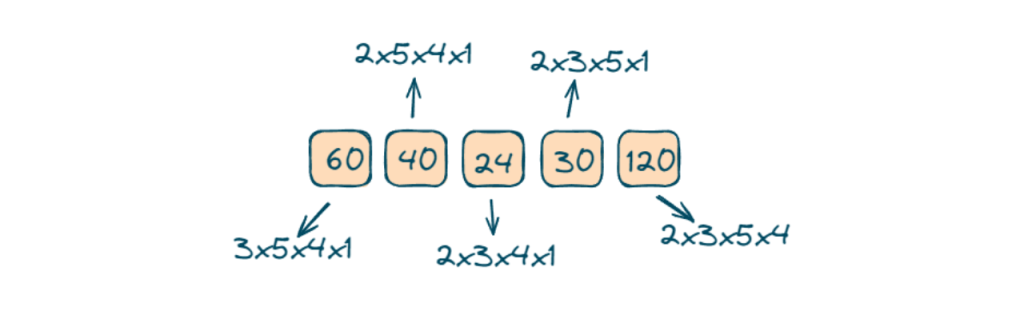
Numbers = [2,3,5,4,1]

Output = [60,40,24,30,120]
For the 0th index, the result will be the product of elements from index 1 to 4, i.e. 3*5*4*1 = 60. Similarly, it is calculated for the rest of the indexes.
Using Prefix and Suffix Arrays to Solve this Problem
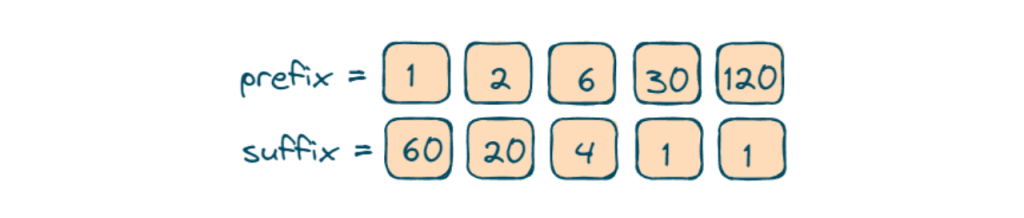
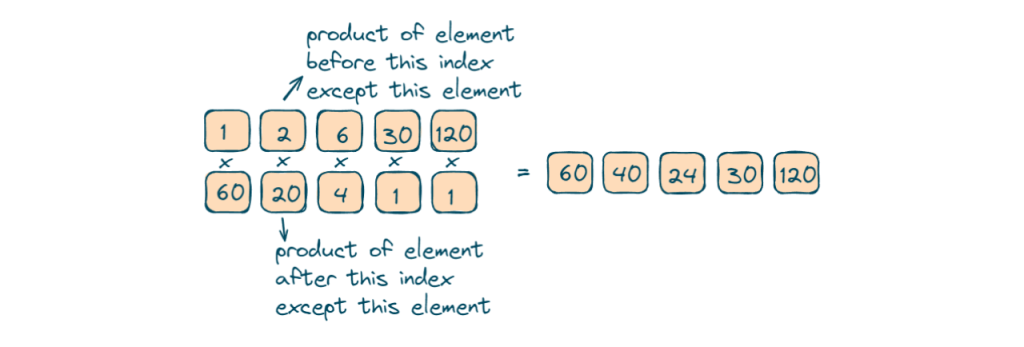
In this approach, we will use a prefix and suffix array in a prefix array. We will maintain the product of the element of the array till that element from the start of the array for every element. In a suffix array, we will maintain the product of the element of the array till that element from the last of the array.
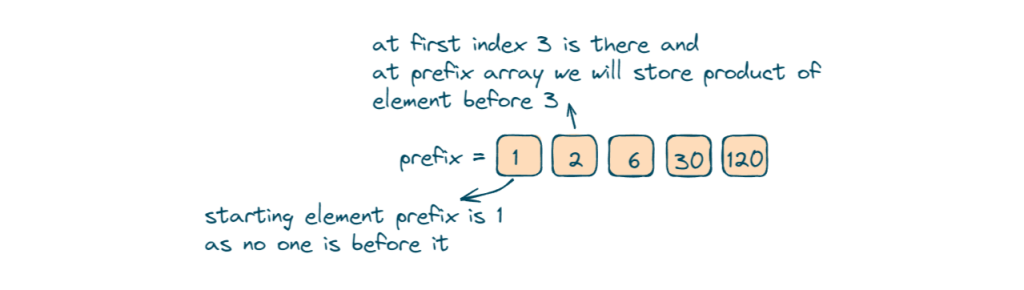
- Firstly we will fill the prefix array starting with initializing the first element of the prefix array as 1, as there are in the beginning there are no initial elements.
- Now we will iterate over the array starting from the second element and calculate the prefix product for that index.
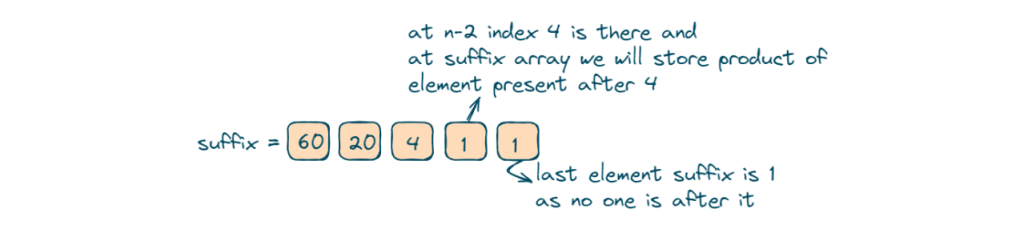
- After the prefix array, we will fill the suffix array starting with initializing the last element as 1, because there are no elements to the right.
- Now we will iterate over the array starting from the second last element to the first element and calculate the suffix product for that index.
- As we have calculated prefixes and suffixes for each index, the product of the prefix of an index and suffix of an index will give us the product of an array except that element.
- Now we will iterate over the prefix array and suffix array and find the product of the array for every element except that current element.
C++ Code
Here is the C++ program to find the product of array except itself:
#include <bits/stdc++.h>
using namespace std;
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
// Initialize arrays to store prefix and suffix products
vector<int> prefix(n, 1); // Prefix product of elements to the left
vector<int> suffix(n, 1); // Suffix product of elements to the right
vector<int> prod(n); // Final product array
// Calculate prefix products
for (int i = 1; i < n; i++) {
prefix[i] = prefix[i - 1] * nums[i - 1];
}
// Calculate suffix products
for (int i = n - 2; i >= 0; i--) {
suffix[i] = suffix[i + 1] * nums[i + 1];
}
// Calculate the final product array
for (int i = 0; i < n; i++) {
prod[i] = prefix[i] * suffix[i];
}
return prod;
}
int main() {
vector<int> nums = {2, 3, 5, 4, 1};
vector<int> prod = productExceptSelf(nums);
cout << "The product array is: ";
for (int num : prod) {
cout << num << " ";
}
cout << endl;
return 0;
}Java Code
Below is the Java program to solve it:
import java.util.Arrays;
public class ProductExceptSelf {
public static int[] productExceptSelf(int[] nums) {
int n = nums.length;
// Initialize arrays to store prefix and suffix products
int[] prefix = new int[n]; // Prefix product of elements to the left
int[] suffix = new int[n]; // Suffix product of elements to the right
int[] prod = new int[n]; // Final product array
// Calculate prefix products
prefix[0] = 1;
for (int i = 1; i < n; i++) {
prefix[i] = prefix[i - 1] * nums[i - 1];
}
// Calculate suffix products
suffix[n - 1] = 1;
for (int i = n - 2; i >= 0; i--) {
suffix[i] = suffix[i + 1] * nums[i + 1];
}
// Calculate the final product array
for (int i = 0; i < n; i++) {
prod[i] = prefix[i] * suffix[i];
}
return prod;
}
public static void main(String[] args) {
int[] nums = {2, 3, 5, 4, 1};
int[] prod = productExceptSelf(nums);
System.out.print("The product array is: ");
System.out.println(Arrays.toString(prod));
}
}Python Code
Here is the implementation in Python as well:
def product_except_self(nums):
n = len(nums)
# Initialize arrays to store prefix and suffix products
prefix = [1] * n # Prefix product of elements to the left
suffix = [1] * n # Suffix product of elements to the right
prod = [0] * n # Final product array
# Calculate prefix products
for i in range(1, n):
prefix[i] = prefix[i - 1] * nums[i - 1]
# Calculate suffix products
for i in range(n - 2, -1, -1):
suffix[i] = suffix[i + 1] * nums[i + 1]
# Calculate the final product array
for i in range(n):
prod[i] = prefix[i] * suffix[i]
return prod
nums = [2, 3, 5, 4, 1]
prod = product_except_self(nums)
print("The product array is:", prod)Output:
The product array is: [60, 40, 24, 30, 120]The time complexity of this approach is O(n) as Calculating the prefix array takes O(n) time, where n is the size of the input array, Calculating the suffix array also takes O(n) time, calculating the product of prefix[i] * sufix[i] array takes O(n) time. So The overall time complexity is O(n).
The space complexity of this approach is O(n)+O(n) as we are using prefix array and suffix array of size n where n is the size of the given array.
Now, you can solve another problem called Subarray Sum Equals K, which is also asked a lot in interviews.
Conclusion
In this article, we have discussed an optimized approach to solve this unique leetcode problem to find the product of array except itself. Using prefix and suffix array limits the time complexity to O(n) without using the division operator