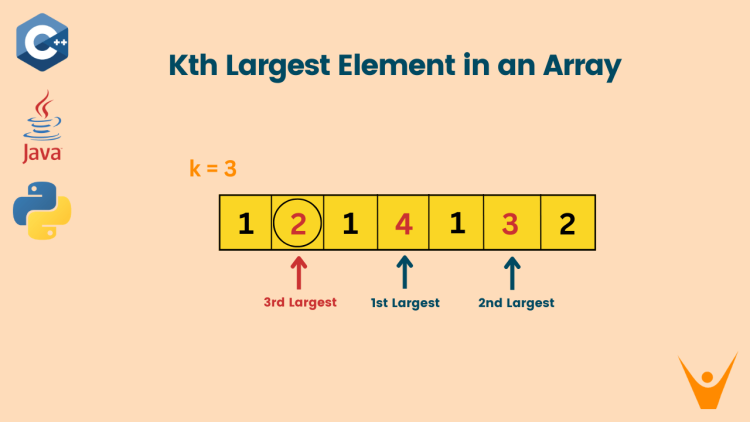
Find Kth Largest Element in an Array (C++, Java, Python)

One of the array problems that is commonly asked in technical interviews is finding the kth largest element in the array. It becomes more challenging when we have to solve it without sorting, in this article we will discuss the optimal approach to solve this problem with implementation in C++, Java, and Python.

What is kth Largest Element Problem?

In this leetcode problem, we have to find the kth largest element in an array, an element that comes in the kth place of the largest element where k is given.

Let us understand it with an example:

Array = [7,4,2,5,3,1]
K = 3
Output = 4

The 1st largest is 7, 2nd largest is 5, and the 3rd largest, i.e. the kth largest is 4.

Optimal Approach using Min-Heap

To find the Kth Largest Element in an Array without sorting we have to use a min-heap and maintain it with size k.

Here are the steps involved:

In the first step, we must declare a priority queue with greater<int>. The greater<int> is a custom comparator that ensures the smallest element on the top.
Now we will iterate through the array and insert each element into the min-heap. We will keep a check that if the size of the min-heap exceeds k then we will remove the smallest element (root) of the min-heap.
- Firstly we will insert 7, 4, 2, and 5 and our min-heap will look like this:

Now after this min-heap will check that size if the size is greater than k then pop an element

Now again an element is inserted in the min-heap

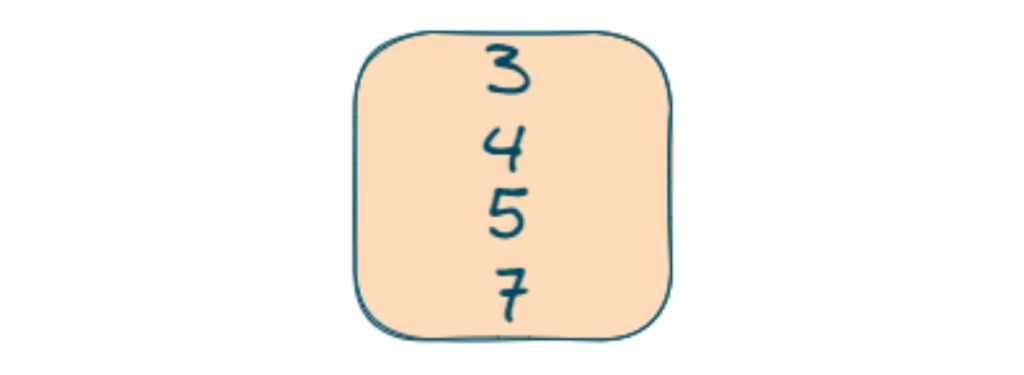
Again min-heap size increased than the k size so we will pop an element

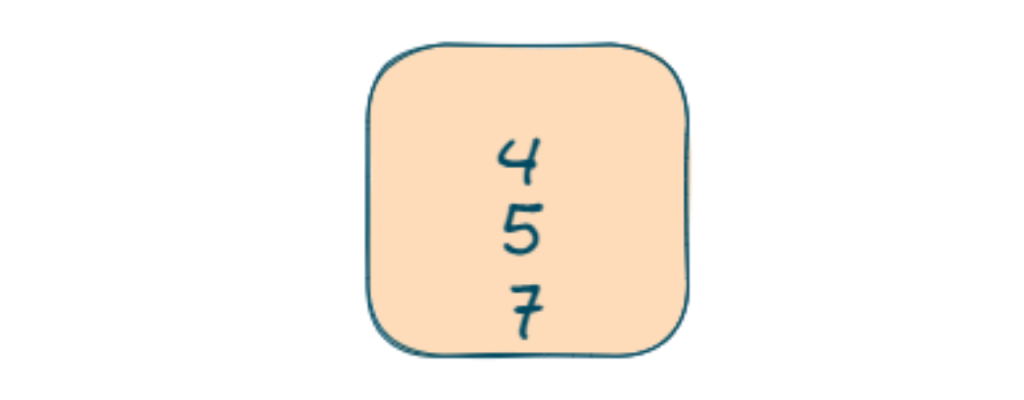
Now 1 is inserted in min-heap

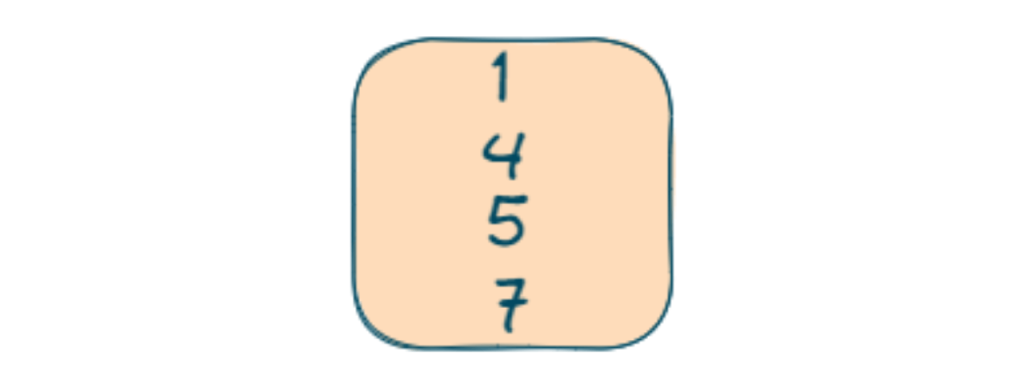
Again min-heap size increased than the k size so we will pop an element and now all elements are iterated once and we have maintained a min heap of size k.
So the root of our min-heap is our kth largest element.
After doing the above step for elements present in the array we will get a min heap of k size and the root of the min-heap is our kth largest element

For example, if we have n number of elements and we have to give nth largest element then we have to return the smallest element present in the array as the same thing we are doing by maintaining k size min-heap.

C++ Code

Here is a C++ program to find the Kth largest element in an array:

#include<bits/stdc++.h>
using namespace std;

int findKthLargest(vector<int>& nums, int k) {
    // Create a min-heap
    priority_queue<int, vector<int>, greater<int>> minHeap;

    // Insert elements into the heap until size reaches k
    for (int num : nums) {
        minHeap.push(num);
        if (minHeap.size() > k) {
            minHeap.pop();  // Maintain size of k
        }
    }

    // The root of the max-heap is the kth largest element
    return minHeap.top();
}

int main() {
    vector<int> nums = {7, 4, 2 , 5, 3, 1};
    int k = 3;

    int result = findKthLargest(nums, k);

    cout << "The " << k << "th largest element is: " << result << endl;

    return 0;
}

Python Code

Here is a Python program as well:

import heapq

def find_kth_largest(nums, k):
    min_heap = []

    for num in nums:
        heapq.heappush(min_heap, num)
        if len(min_heap) > k:
            heapq.heappop(min_heap)

    return min_heap[0]

# Example usage
nums = [7, 4, 2, 5, 3, 1]
k = 3
result = find_kth_largest(nums, k)
print(f"The {k}th largest element is: {result}")

Java Code

You can implement it in Java for Min-Heap approach also:

import java.util.PriorityQueue;

public class KthLargestElement {
    public static int findKthLargest(int[] nums, int k) {
        // Create a min-heap
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        // Insert elements into the heap until size reaches k
        for (int num : nums) {
            minHeap.offer(num);
            if (minHeap.size() > k) {
                minHeap.poll(); // Maintain size of k
            }
        }

        // The root of the max-heap is the kth largest element
        return minHeap.peek();
    }

    public static void main(String[] args) {
        int[] nums = {7, 4, 2, 5, 3, 1};
        int k = 3;

        int result = findKthLargest(nums, k);

        System.out.println("The " + k + "th largest element is: " + result);
    }
}

Output:

The 3th largest element is: 4

Complexity Analysis

The time complexity for this is O(n*logK) where n is the size of an array and k is the element we have to return. Firstly we are iterating through arrays and inserting elements in a min-heap.

The space complexity is O(k) because the space used by the min-heap is of k size only in the worst case if k = n then space complexity is equal to O(k).

Conclusion

In this article, we have learned that the min-heap-based approach provides an efficient solution for finding the kth largest element without explicitly sorting the entire array. It is particularly beneficial when k is significantly smaller than the size of the array, optimizing both time and space complexity.

There are many other array problems you might have to practice, and if you face any hurdle, our data structures tutors are available 24×7 online!