Adding two numbers gives us the nostalgia for being in primary school. From counting the numbers on our fingers to counting the nodes of a linked list, we have all grown in different ways. To take one step further in the world of linked lists, we will be looking at a frequently asked problem: Add two numbers represented by linked lists. This article will discuss the various approaches, ranging from brute force to the most optimized ones, along with their complexities and codes.
“Add Two Numbers” Problem Statement
In this problem, we are given two non-empty linked lists. Each linked list represents a number with its digits stored in reverse order, such that each node contains one digit. We need to add these numbers and then return the sum in the form of a new linked list.
Note: The numbers do not contain any leading zeroes, For eg. 000089.
Let’s understand this with an example.
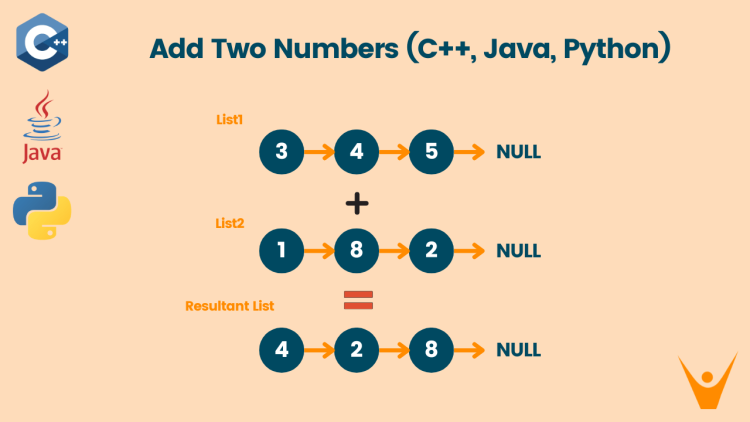
Input:
list1 = [ 3, 4, 5 ]
list2 = [ 1, 8, 2 ]Output:
sum = [ 4, 2, 8 ]Explanation:
List1 represents the number 543, as it is stored in reverse order, and list2 represents the number 281, so the sum of both numbers is 543 + 281, i.e. 824. So the output is [ 4, 2, 8 ] in reverse order in the form of a linked list.
Brute Force Approach
The easiest way to solve this problem is by traversing both lists and obtaining the number out of the lists. We can then add the number to get the sum and form the resultant linked list. Seems easy? Let’s see the steps on how we can do it:
- Initialize two integers num1 and num2 with 0.
- Traverse both linked lists one by one and apply simple mathematics, i.e, add the value of the node to the number and multiply the number by 10.
- Add both numbers to get their sum.
- Initialize a new node as head and take one temp node to create each digit and push it to the linked list.
- Now create the resultant linked list by using simple calculations, i.e., ( sum%10 ) to get the digit and ( sum/10 ) to get the remaining digits.
- Repeat the above step until the sum >0.
The time complexity for this solution will be O(m+n), where m and n are the lengths of the respective linked lists. As we are traversing each of the linked lists to obtain the desired numbers.
Optimal Approach
The naive approach requires us to traverse each linked list one by one and then add them to obtain the result. But we can reduce this complexity of two loops by traversing both lists at once and simultaneously adding the digits to obtain the sum. Thus, we can create the resultant linked list on the fly.
Algorithm
We can follow these simple steps to solve it using the optimal approach:
- Initialize two integers, digit and carry. The digit will hold the least significant digit of the sum and carry holds the digit that overflows.
- Create a dummy node, head. It represents the head of the new linked list and we will use it to print the linked list.
- Now, we need to traverse both lists at once, So we initialize temp1 and temp2 pointers to head1 and head2 of the lists.
- We will loop through the lists and perform the following operations:
- Calculate the Sum = temp1->val + temp2->val + carry.
- To find the least significant digit and carry, digit = sum%10 and carry = sum/10.
- Create a new node and set its value as the digit.
- Set this node as the next of the temp pointer, to assign it to the tail of the linked list.
- Increment all three-pointers, temp, temp1, and temp2.
- Handle the case when the length of one list is greater than the other by looping through the larger list and assigning each digit to the sum.
Let’s perform the above steps in this example:
Iteration 1: temp1 → val = 3, temp2 → val = 1, Carry = 0
First add these to get the Sum, i.e. 3 + 1 + Carry ( 0 ) = 4
Now, Digit = 4 and Carry = 0.
Iteration 2: temp1 → val = 4, temp2 → val = 8, Carry = 0
First add these to get the Sum, i.e. 4 + 8 + Carry ( 0 ) = 12
Now, Digit = 2 and Carry = 1.
Iteration 3: temp1 → val = 5, temp2 → val = 2, Carry = 1
First add these to get the Sum, i.e. 5 + 2 + Carry ( 1 ) = 8
Now, Digit = 8 and Carry = 0.
Since both the lists are traversed, this is our resultant linked list.
C++ Code
#include <bits/stdc++.h>
using namespace std;
class ListNode{
public:
int val;
ListNode* next;
ListNode(int val){
this->val = val;
this->next = NULL;
}
};
ListNode* addTwoList(ListNode* temp1, ListNode* temp2){
int sum = 0, carry = 0, digit = 0;
ListNode* head = new ListNode(0);
ListNode* temp = head;
while(temp1 and temp2){
sum = temp1->val + temp2->val + carry;
carry = sum/10;
digit = sum%10;
temp->next = new ListNode(digit);
temp1 = temp1->next;
temp2 = temp2->next;
temp = temp->next;
}
while(temp1){
sum = temp1->val + carry;
carry = sum/10;
digit = sum%10;
temp->next = new ListNode(digit);
temp1 = temp1->next;
temp = temp->next;
}
while(temp2){
sum = temp2->val + carry;
carry = sum/10;
digit = sum%10;
temp->next = new ListNode(digit);
temp2 = temp2->next;
temp = temp->next;
}
if(carry){
temp->next = new ListNode(carry);
}
return head->next;
}
void print(ListNode *head){
ListNode* temp = head;
while(temp){
cout<<temp->val<<" ";
temp = temp->next;
}
cout<<endl;
}
int main() {
ListNode* head1 = new ListNode(3);
head1->next = new ListNode(4);
head1->next->next = new ListNode(5);
cout<<"List1: ";
print(head1);
ListNode* head2 = new ListNode(1);
head2->next = new ListNode(8);
head2->next->next = new ListNode(2);
cout<<"List2: " ;
print(head2);
ListNode* newhead = addTwoList(head1, head2);
cout<<"Resultant List: ";
print(newhead);
return 0;
}Java Code
class ListNode {
public int val;
public ListNode next;
public ListNode(int val) {
this.val = val;
this.next = null;
}
}
public class Main {
public static ListNode addTwoLists(ListNode temp1, ListNode temp2) {
int sum = 0, carry = 0, digit = 0;
ListNode head = new ListNode(0);
ListNode temp = head;
while (temp1 != null && temp2 != null) {
sum = temp1.val + temp2.val + carry;
carry = sum / 10;
digit = sum % 10;
temp.next = new ListNode(digit);
temp1 = temp1.next;
temp2 = temp2.next;
temp = temp.next;
}
while (temp1 != null) {
sum = temp1.val + carry;
carry = sum / 10;
digit = sum % 10;
temp.next = new ListNode(digit);
temp1 = temp1.next;
temp = temp.next;
}
while (temp2 != null) {
sum = temp2.val + carry;
carry = sum / 10;
digit = sum % 10;
temp.next = new ListNode(digit);
temp2 = temp2.next;
temp = temp.next;
}
if (carry != 0) {
temp.next = new ListNode(carry);
}
return head.next;
}
public static void print(ListNode head) {
ListNode temp = head;
while (temp != null) {
System.out.print(temp.val + " ");
temp = temp.next;
}
System.out.println();
}
public static void main(String[] args) {
ListNode head1 = new ListNode(3);
head1.next = new ListNode(4);
head1.next.next = new ListNode(5);
System.out.print("List1: ");
print(head1);
ListNode head2 = new ListNode(1);
head2.next = new ListNode(8);
head2.next.next = new ListNode(2);
System.out.print("List2: ");
print(head2);
ListNode newhead = addTwoLists(head1, head2);
System.out.print("Resultant List: ");
print(newhead);
}
}Python Code
class ListNode:
def __init__(self, val):
self.val = val
self.next = None
def add_two_lists(temp1, temp2):
sum_val, carry, digit = 0, 0, 0
head = ListNode(0)
temp = head
while temp1 and temp2:
sum_val = temp1.val + temp2.val + carry
carry = sum_val // 10
digit = sum_val % 10
temp.next = ListNode(digit)
temp1 = temp1.next
temp2 = temp2.next
temp = temp.next
while temp1:
sum_val = temp1.val + carry
carry = sum_val // 10
digit = sum_val % 10
temp.next = ListNode(digit)
temp1 = temp1.next
temp = temp.next
while temp2:
sum_val = temp2.val + carry
carry = sum_val // 10
digit = sum_val % 10
temp.next = ListNode(digit)
temp2 = temp2.next
temp = temp.next
if carry:
temp.next = ListNode(carry)
return head.next
def print_list(head):
temp = head
while temp:
print(temp.val, end=" ")
temp = temp.next
print()
if __name__ == "__main__":
head1 = ListNode(3)
head1.next = ListNode(4)
head1.next.next = ListNode(5)
print("List1: ", end="")
print_list(head1)
head2 = ListNode(1)
head2.next = ListNode(8)
head2.next.next = ListNode(2)
print("List2: ", end="")
print_list(head2)
new_head = add_two_lists(head1, head2)
print("Resultant List: ", end="")
print_list(new_head)Output:
List1: 3 4 5
List2: 1 8 2
Resultant List: 4 2 8The time complexity for this approach is O(max(m,n))), where m and n are the lengths of the respective linked lists. Since we are traversing both lists at once, the maximum time required will be the max of the lengths of both.
The space complexity is O(max(m,n)), as the resultant linked list will be of the size of the number of digits in the sum, which is a maximum of m, n and a carry of 1.
Conclusion
Adding two numbers represented by the linked lists is an interesting problem and is asked frequently in the interviews. We can solve it using 2 different approaches as discussed in this article.