A binary search tree, or BST. stores the values in such a way that if we write the inorder of that tree it will be in ascending order. This can be achieved if the value of a left node is smaller and the value of the right node is greater or equal to the parent node. Different types of questions are asked in interviews based on BST, but we will discuss how to find the kth smallest element in the BST.
What is the “kth Smallest element in the BST”?
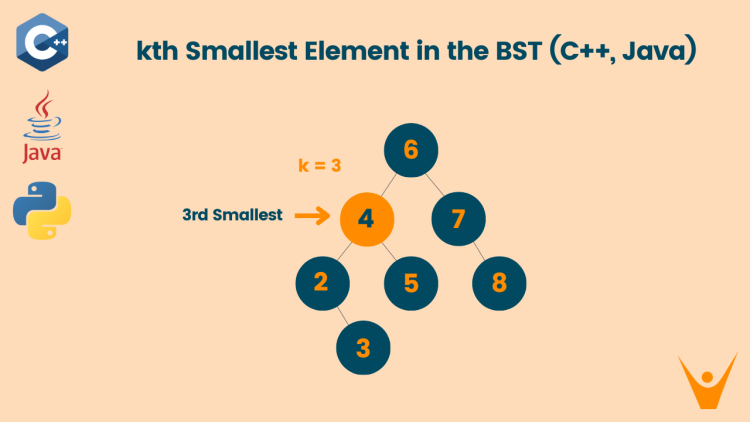
In this problem, you have to find the kth smallest element from a given binary search tree. K is always smaller or equal to the total number of nodes in the tree. Let’s look at an example to learn more.
In the given tree the 3rd smallest element is 5.
The basic approach is to store the values of nodes in an array. Then sort the array and find the kth smallest value from this.
Let’s examine this with an example:
• Create an array
• Traverse each node in the tree and store their values in the array.
• Sort the array.
• Return the value present at the k-1 index of the array.
The time complexity of the code is O( n log(n) ) where n is the total number of elements present in the array. This is because we are sorting the array and sorting required (n log(n)) time complexity. Space complexity is O(n) because we are using an array to store all the values of the tree.
Inorder Traversal Approach to Find It
In the above approach, we are sorting the array which increases our time complexity to O( n log(n)). Also in the above approach space required is around O(n) which can be reduced if we use the inorder traversal.
The steps for the inorder traversal approach to find kth smallest element in BST are:
- First, traverse the left node.
- Update the current value of the count variable to count + 1.
- If the value of count becomes equal to k then print this value and return.
- If not go for the right node of the current node.
- If at any point the node is Null then, return.
C++ Code
Here is the C++ program to find kth smallest element in BST:
#include <bits/stdc++.h>
using namespace std;
class node{
public:
int value;
node* left;
node* right;
node(){
left = NULL;
right = NULL;
}
node(int x){
value = x;
left = NULL;
right = NULL;
}
};
// variable that stores the kth smallest value
int ans = -1;
// function that is doing inorder traversal
void fun(node* root, int& count, int k){
if(root==NULL) return ;
fun(root->left,count,k);
count++;
if(count==k){
ans = root->value;
return;
}
fun(root->right,count,k);
return;
}
int main(){
// creating a tree
// 5
// / \
// 3 7
// / \ \
// 1 4 9
node* head = new node(5);
head->left = new node(3);
head->right = new node(7);
head->left->left = new node(1);
head->left->right = new node(4);
head->right->right = new node(9);
// k is 5, so the 5th smallest value is 7 here
// 1 -> 1
// 2 -> 3
// 3 -> 4
// 4 -> 5
// 5 -> 7
// 6 -> 9
int k = 5;
int count = 0;
fun(head,count,k);
// prints 7
cout<<k<<"th smallest values is: "<<ans<<endl;
return 0;
}Java Code
Here is the Java program to find it:
class Node {
int value;
Node left, right;
Node(int x) {
value = x;
left = right = null;
}
}
class KthSmallestValue {
// variable that store the kth smallest value
static int[] ans = {-1};
// function that is doing inorder traversal
static void fun(Node root, int[] count, int k) {
if (root == null)
return;
fun(root.left, count, k);
count[0]++;
if (count[0] == k) {
ans[0] = root.value;
return;
}
fun(root.right, count, k);
}
public static void main(String[] args) {
// creating a tree
// 5
// / \
// 3 7
// / \ \
// 1 4 9
Node head = new Node(5);
head.left = new Node(3);
head.right = new Node(7);
head.left.left = new Node(1);
head.left.right = new Node(4);
head.right.right = new Node(9);
// k is 5, so the 5th smallest is value is 7 here
// 1 -> 1
// 2 -> 3
// 3 -> 4
// 4 -> 5
// 5 -> 7
// 6 -> 9
int k = 5;
int[] count = {0};
fun(head, count, k);
// prints 7
System.out.println(k + "th smallest values is: " + ans[0]);
}
}Python Code
You can do the same in Python also:
class Node:
def __init__(self, x):
self.value = x
self.left = None
self.right = None
# variable that stores the kth smallest value
ans = [-1]
# function that is doing inorder traversal
def fun(root, count, k):
if root is None:
return
fun(root.left, count, k)
count[0] += 1
if count[0] == k:
ans[0] = root.value
return
fun(root.right, count, k)
def main():
# creating a tree
# 5
# / \
# 3 7
# / \ \
# 1 4 9
head = Node(5)
head.left = Node(3)
head.right = Node(7)
head.left.left = Node(1)
head.left.right = Node(4)
head.right.right = Node(9)
# k is 5, so the 5th smallest is value is 7 here
# 1 -> 1
# 2 -> 3
# 3 -> 4
# 4 -> 5
# 5 -> 7
# 6 -> 9
k = 5
count = [0]
fun(head, count, k)
# prints 7
print(f"{k}th smallest values is: {ans[0]}")
if __name__ == "__main__":
main()Output:
7As we are just iterating the values of the tree so in the worst case time complexity will be O(n). If the element is present at the last. Space complexity will reduced to O(1) as no extra space is required.
We can compare both the approach to check which one is better:
| Approach | Time Complexity | Space Complexity | Description |
|---|---|---|---|
| Brute Force | O(n Log(n)) | O(n) | We are sorting the array which requires log(n) time complexity. Also, we are sorting the values in the array which requires O(n) space complexity. |
| Optimized Approach | O(n) | O(1) | We are only traversing the tree once. |
Conclusion
In this article, we learned how to find the kth smallest element of a Binary Search Tree. Some other important problems asked in interviews are how to delete node in BST, perform zig-zag traversal, and print the top view of a binary tree.