Claude 3’s latest feature lets users create animations thus allowing them to explore and understand complicated mathematics topics using visuals. Here’s a guide to creating Maths animations like Sphere Theorem, Distance Formula, and Riemann Sum using Claude 3 and Manim!
Claude 3’s Math Animations Feature
Claude 3 has introduced support for Manim Animation Engine, designed specifically for mathematical animations.
Manim is an open-source, community-maintained Python library that is used for creating explanatory math videos using animations and writing just a few lines of code. With this integration, users can understand various complex problems in mathematics using simple but stunning visuals.
A video showing the animation of the Pythagoras theorem generated by Claude is causing waves all over the internet. You can take a look at how Claude functions with Manim in the video below:
Ok, this is amazing.
— Alvaro Cintas (@dr_cintas) March 12, 2024
I asked Claude 3 to generate an animation of the Pythagorean Theorem and this is what it created: pic.twitter.com/bM4oDbyEbv
The user asked Claude to explain the Pythagoras theorem with the help of visuals. Claude then uses the manim library and provides the user with a simple explanation of the theorem in a short video.
It excels at designing animations for any mathematical concept, although its accuracy may not be flawless. The possible use cases will be to create educational videos, presentations, visualization of algorithms, and simulations.
How to Generate Animations with Claude 3?
Claude AI is slowly sending out its new Manim update to all users. For those who have access to Manim in Claude, this is how they can use it:
- Go to claude.ai.
- Enter the prompt in the following template pattern:
- Mathematical Expression/Concept: Animate the process of finding the derivative of the function f(x) = x^3 + 2x^2 – 3x using the power rule.
- Additional Context: Show the step-by-step process of applying the power rule to each term of the function and Highlight the original function and the resulting derivative function.
- Specific Requests: Use a clean and minimalist style with a white background and Color-code the different terms and coefficients for clarity.
- Desired Output: Please provide the complete Python script using
manimto create the animation. - Additional Requirements: Include instructions on how to run the animation locally or on platforms like Google Colab.
- Claude provides the Python code for the required concept.
As of now, Claude doesn’t have support to render animations just yet, there are two ways to visualize the animation.
Run the Code Locally
First, Install the Manim library by running the following command:
pip install manimlibCreate the Python script ‘script.py’ and import the necessary classes from the manim lib. For example:
from manim import *
class EquationAnimation(Scene):
def construct(self):
equation = MathTex(r"x^2 + y^2 = z^2")
self.play(Write(equation))
self.wait()To render the animation and generate the video, run the following command in the command prompt or terminal on your local machine
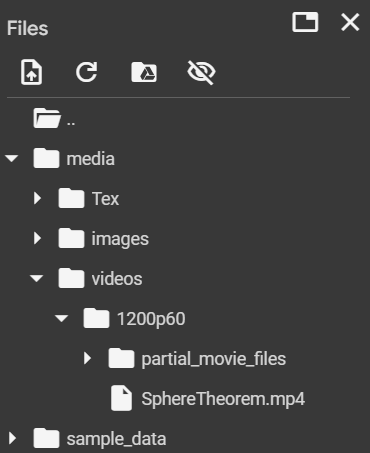
python -m manim path/to/your/script.py EquationAnimation -plTo run this animation, you can find the video in your current working directory in the media/videos/ directory.
On a platform like Google Colaboratory
Upload the Python script to Google Colab or create a new notebook.
Install the following dependencies for running the manim animation.
!apt-get install -qq sox libcairo2 libpango1.0-dev ffmpeg > /dev/null
!pip install -qq manimImport the necessary classes from Manim.
To render the animation, run the following code in a code cell. The render() method runs the animation and saves the video on Google Colab.
from manim import *
# Define your Scene class
class EquationAnimation(Scene):
def construct(self):
equation = MathTex(r"x^2 + y^2 = z^2")
self.play(Write(equation))
self.wait()
# Render the animation
scene = EquationAnimation()
scene.render()To display the rendered video, you can use the IPython.display module in Colab or download the video from the media/videos/ directory in the folder structure.
from IPython.display import Video
Video("EquationAnimation.mp4")Let’s take a look at a few examples!
Example 1: Sphere Theorem
In this example, we will try to animate the popular Sphere Theorem. The Sphere Theorem states that The surface area of a sphere is equal to the area of its circumscribing cylinder’s curved surface.
Prompt:
Animate the process of the Sphere theorem in mathematics
Show the step by step process of the theorem
Use a clean and minimalist style with a white background
Color-code the variables appropriately
Please Provide the complete Python Script using 'manim' to create the animation
Include appropriate code so that I can run it in Google ColabResponse:

Python code:
from manim import *
class Disc(VGroup):
def __init__(self, radius, **kwargs):
super().__init__(**kwargs)
self.radius = radius
circle = Circle(radius=radius, **kwargs)
self.add(circle)
class SphereTheorem(Scene):
def construct(self):
# Create a sphere
sphere = Sphere(radius=2, resolution=(24, 48), fill_opacity=0.5, fill_color=BLUE_E, stroke_width=4, stroke_color=WHITE)
self.play(DrawBorderThenFill(sphere))
self.wait()
# Label the radius
r = MathTex("r", color=GREEN_B).next_to(sphere, LEFT)
self.play(Write(r))
self.wait()
# Show the equation
equation = MathTex(r"V = \frac{4}{3}\pi r^3", color=WHITE).to_edge(UP)
self.play(Write(equation))
self.wait()
# Create a cylinder with the same radius and height
cylinder = Cylinder(height=4, radius=2, resolution=(24, 48), fill_opacity=0.5, fill_color=YELLOW_D, stroke_width=4, stroke_color=WHITE)
self.play(DrawBorderThenFill(cylinder))
self.wait()
# Label the height
h = MathTex("h", color=RED_B).next_to(cylinder, RIGHT)
self.play(Write(h))
self.wait()
# Show the equation for the cylinder's volume
cylinder_equation = MathTex(r"V = \pi r^2 h", color=WHITE).next_to(equation, DOWN)
self.play(Write(cylinder_equation))
self.wait()
# Slice the sphere into horizontal discs
discs = VGroup(*[
Disc(radius=2 * np.cos(theta), fill_opacity=0.5, fill_color=PURPLE_A, stroke_width=2, stroke_color=WHITE)
for theta in np.linspace(0, PI / 2, 12)
])
self.play(DrawBorderThenFill(discs))
self.wait()
# Rearrange the discs to form a cylinder
discs.arrange(DOWN, buff=0)
self.play(Transform(discs, cylinder))
self.wait()
# Show the relationship between the sphere's volume and the cylinder's volume
relationship = MathTex(r"\frac{V_{\text{sphere}}}{V_{\text{cylinder}}} = \frac{4}{3}", color=WHITE).next_to(cylinder_equation, DOWN)
self.play(Write(relationship))
self.wait()
# To run the animation locally
# with tempconfig({"quality": "low_quality"}):
# scene = SphereTheorem()
# scene.render()
# To run the animation on Google Colab
scene = SphereTheorem()
scene.render()
To access the video, look into Colab’s folder structure:
Here is the video:
Here is an animation of the Sphere Theorem: pic.twitter.com/6BfRVIdeOh
— dhruv (@_dhruvvvvv_) March 19, 2024
We observe that although it provides a partial description of the theorem, it fails to deliver a comprehensive explanation as requested by the user.
Example 2: Distance Formula
Another way to understand a math problem is by providing Claude with the problem’s image and the prompt. Claude analyses the image and tries to give the best possible animation for it.
Let’s take an example of the distance formula. The distance formula is used to find the distance between any two points.
Prompt:

Response:
from manim import *
class DistanceFormula(Scene):
def construct(self):
# Set up the scene
self.camera.background_color = BLACK
axes = Axes(
x_range=[-4, 4, 1],
y_range=[-3, 3, 1],
x_length=6,
y_length=5,
tips=False,
)
axes_labels = axes.get_axis_labels()
self.play(Create(axes), Write(axes_labels))
# Create points (x1, y1) and (x2, y2)
point1 = Dot([-2, 1, 0], radius=0.08, color=RED)
point2 = Dot([1, -1, 0], radius=0.08, color=GREEN)
point1_label = MathTex("(x_1, y_1)", color=RED).next_to(point1, LEFT)
point2_label = MathTex("(x_2, y_2)", color=GREEN).next_to(point2, RIGHT)
# Draw the distance line between the points
distance_line = Line(point1.get_center(), point2.get_center(), color=YELLOW)
# Show the distance formula
formula = MathTex(
r"d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}",
color=BLUE
).to_edge(UP)
# Substitute the point coordinates into the formula
substituted_formula = MathTex(
r"d = \sqrt{(1 - (-2))^2 + (-1 - 1)^2}",
color=PURPLE
).next_to(formula, DOWN)
# Evaluate the formula
result = MathTex(r"d = \sqrt{9 + 4} = \sqrt{13}", color=GREEN).next_to(substituted_formula, DOWN)
# Animate objects
self.play(
DrawBorderThenFill(point1),
DrawBorderThenFill(point2),
Write(point1_label),
Write(point2_label),
DrawBorderThenFill(distance_line),
Write(formula),
Write(substituted_formula),
Write(result)
)
self.wait()
# Run the scene
scene = DistanceFormula()
scene.render()Video:
I also provided it with the Distance Formula’s image and got this animation for it: pic.twitter.com/p8CaV1zmXb
— dhruv (@_dhruvvvvv_) March 19, 2024
The output we got from Claude 3 is:

However, all the animations still aren’t entirely perfect. Some animations are not very descriptive and don’t convey a lot of meaning to the user.
Example 3: Riemann Sum Theorem
Let us consider the Riemann Sum theorem. This theorem provides a method for approximating the area under a curve by dividing the interval into smaller subintervals and summing the areas of corresponding rectangles. Claude was prompted with the sample image and told to explain the theorem.

Python code:
from manim import *
class RiemannSum(Scene):
def construct(self):
# Create the axes
axes = Axes(
x_range=[0, 4, 1],
y_range=[0, 5, 1],
x_length=6,
y_length=6,
axis_config={"include_tip": False},
tips=False,
)
self.play(Create(axes))
self.wait()
# Define the function
func = lambda x: 4 * (1 - x / 4) ** 2
curve = axes.plot(func, color=BLUE)
self.play(Create(curve))
self.wait()
# Show the Riemann Sum equation
riemann_sum_equation = MathTex(r"\sum_{i=1}^{n} f(x_i^*) \Delta x", color=WHITE).to_edge(UP)
self.play(Write(riemann_sum_equation))
self.wait()
# Create the rectangles
rectangles = VGroup()
n = 4 # Number of rectangles
dx = 4 / n # Width of each rectangle
for i in range(n):
x = i * dx
y = func(x)
rect = Rectangle(
width=dx,
height=y,
stroke_color=WHITE,
fill_color=YELLOW,
fill_opacity=0.5,
)
rect.move_to(axes.c2p(x + dx / 2, y / 2))
rectangles.add(rect)
self.play(DrawBorderThenFill(rectangles))
self.wait()
# Animate the rectangles
for rect in rectangles:
self.play(rect.animate.stretch_to_fit_height(axes.p2c(rect.get_center())[1]), run_time=0.5)
self.wait(0.5)
self.wait(2)
# To run the animation locally
# with tempconfig({"quality": "low_quality"}):
# scene = RiemannSum()
# scene.render()
# To run the animation on Google Colab
scene = RiemannSum()
scene.render()
Here’s the response we got:

Claude’s explained the theorem and gave the correct formula but the animation couldn’t provide any clarity. This is not useful for the user who wants a clear explanation of the theorem.
I then provided it with a sample image and asked to explain the theorem (Riemann Sum): pic.twitter.com/ViKcY8Y7Mn
— dhruv (@_dhruvvvvv_) March 19, 2024
While not always accurate, these animations are still useful in explaining concepts to users.
Conclusion
AI’s mastery of math algorithms, pattern recognition, data understanding, and precision in generating animations is a process that will still require time. Nevertheless, this addition to Claude will revolutionize automation within the mathematics industry by enabling the creation of diverse tutorials with minimal input








